浮点数
在计算机科学中,浮点是一种对实数近似值的表现方法,有一个尾数(即小数)加上阶码(即指数)来表示,通常是乘以某个基数的指数次。使用这种办法表示的数值成为浮点数。计算机中一般采用二进制为基,加上固定的精度来表示浮点。
\begin{equation} f = \pm m \times b^{ \pm e } \end{equation}
此外,浮点数表示法通常还包括一些特别的数值:+∞ 和 −∞(正负无穷大)以及 NaN(Not a Number)。无穷大用于数太大而无法表示的时候,NaN 则指示非法操作或者无法定义的结果。其中,无穷大,可表示为inf,在内存中的值是阶码为全1,尾数全0。而NaN在内存中的值则是阶码全1,尾数不全0。
通常情况下,在电脑中使用的浮点规范为 IEEE 754。
IEEE 754
IEEE二进制浮点数算术标准(IEEE 754)是20世纪80年代以来最广泛使用的浮点数运算标准,为许多CPU与浮点运算器所采用。该标准的全称为IEEE二进制浮点数算术标准(ANSI/IEEE Std 754-1985),又称IEC 60559:1989,微处理器系统的二进制浮点数算术(本来的编号是IEC 559:1989)[1]。后来还有“与基数无关的浮点数”的“IEEE 854-1987标准”,有规定基数为2跟10的状况。现在最新标准是“ISO/IEC/IEEE FDIS 60559:2010”。
标准主要定义了下面的内容:
- 浮点数的格式
- 反常值(denormal number)
- 一些特殊数值(无穷(Inf)与非数值(NaN))
- 以及这些数值的“浮点数运算符”
- 四种数值舍入规则
- 五种例外情况
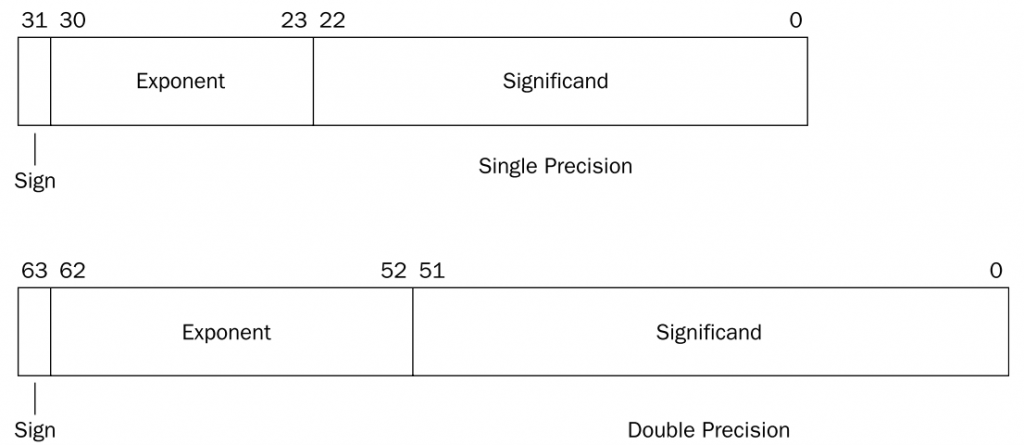
同时,标准还规定了四种浮点数的表示方式:单精确度(32位)、双精确度(64位)、延伸单精确度(43比特以上,很少使用)与延伸双精确度(79比特以上,通常以80比特实做)。
存储格式
IEEE 754 规定二进制了浮点数的存储格式:
+----------------------------+
| sign | exponent | fraction |
+----------------------------+
e+f+1 e+f f 0
其中最高位为符号位,紧接着的 e 个 bit 存储指数部分,剩 f 个 bit 则表示小数部分。
需要注意的是 IEEE 754 的指数部分有一个指数偏移值,标准规定该值为:$ 2^{e - 1}-1 $。
指数偏移值(exponent bias),是指浮点数表示法中的指数域的编码值为指数的实际值加上某个固定的值。
以单精度为例,指数部分长度为 8 ,如果编码值为 128,那么实际值应该为 128 - 127 = 1
采用指数的实际值加上固定的偏移值的办法表示浮点数的指数,好处是可以用长度为e个比特的无符号整数来表示所有的指数取值,这使得两个浮点数的指数大小的比较更为容易,实际上可以按照字典序比较两个浮点表示的大小。这种移码表示的指数部分,中文称作阶码。如果不能理解,可以参考一张图看懂原码、反码、补码、移码。
浮点数的“规约”
浮点数中存在多种表示为相同值的情况,比如:
\begin{equation} 0.1 \times 10^2 = 0.01 \times 10^3 \end{equation}
为了统一,将指数部分的编码值在 $ 0 < exponent < 2^{e}-2 $ 之间,且尾数部分最高有效位(即整数字)是1的浮点数将被称为规约形式的浮点数。“规约”是指用唯一确定的浮点形式去表示一个值。
因为最高位始终为1,所以实际编码中可以省略,称为隐含的二进制有效数字,而 IEEE 754 称这种编码方式的尾数为有效数(significant)。
显然,有规约形式就有非规约形式,但是并非所以不是规约形式的浮点数都叫做非规约形式哦。非规约形式的浮点数(Denormalized Number):规格浮点约定小数点前一位默认是1,而非规格浮点约定小数点前一位可以为0,这样小数精度就相当于多了最多2^22范围。可以看到,非规约形式的浮点数实际上也是“规约”的。IEEE 754 标准规定:非规约形式的浮点数的指数偏移值比规约形式的浮点数的指数偏移值大1。实际上非规约形式的浮点数比规约形式的浮点数更接近与 0 。如果不能理解为甚么有“规约”的非规约形式浮点数,可以参考你应该知道的浮点数基础知识。
浮点数比较
通过规约化形式和指数偏移,浮点数基本上可以按照符号位、指数域、尾数域的顺序作字典比较。显然,所有正数大于负数;正负号相同时,指数的二进制表示法更大的其浮点数值更大;指数相同则比较尾数部分的大小。
这里有三个特殊值需要指出:
- 如果指数是0并且尾数的小数部分是0,这个数 ±0(和符号位相关)
- 如果指数 $ 2^{e}-1 $ 并且尾数的小数部分是0,这个数是 ±∞(同样和符号位相关)
- 如果指数 $ 2^{e}-1 $ 并且尾数的小数部分非0,这个数表示为不是一个数(NaN)
此时有:
- -Inf < 负的规约浮点数数 < 负的非规约浮点数 < -0.0 = 0.0 < 正的非规约浮点数 < 正的规约浮点数 < Inf
- -inf = -inf, inf = inf, NaN 与任何浮点数(包括自身)的比较结果都为假,即 (NaN ≠ x) = false.
编程语言中的浮点数
如果 ISO C 有预定义 __STDC_IEC_559__ 时支持 IEC 60559:1989 (IEEE 754) 指定的浮点数,C++下则是浮点类型对应 numeric_limits 的 is_iec559 为 true 时。此时 float 和 double 浮点型分别对应的是单精度和双精度浮点数。
references
[1] 浮点数 - wiki [2] IEEE 754 - wiki